Занимательная геометрия для любознательного лыжника

Reports Лента автора 3 Сентября 2007 (03:44) Просмотров: 252 0

Начало

Часть 2

В первой части мы посмотрели на поверхности, которые получаются из лыжи при сделанных нами допущениях, и убедились, что такая лыжа имеет ряд особенностей, которые проистекают из геометрии поверхности и вряд ли могут быть отнесены к достоинствам лыжи. С другой стороны, и недостатками их не хотелось бы называть, поскольку никакой количественной оценки степени их влияния на поведение лыжи нет. Может, она где-то в десятом знаке после запятой. С третьей стороны, заниматься их количественной оценкой автору хотелось бы ещё меньше. Поэтому пусть так и останутся «особенностями». Но естественно возникает вопрос: а нет ли такой подходящей для лыжи поверхности, которая была бы от этих особенностей свободна?

Ну, не зря же мы древнегреческих греков упоминали! Они много чего изобрели. И всяких поверхностей у них – до страсти. Есть из чего выбирать. Вот мы и выберем что-нибудь простенькое, без претензий. А именно поверхность прямого кругового конуса. Подходящий от неё кусок. Коническая поверхность хороша уж тем, что имеет плоскую развёртку, и мы пока не хотим (пока, потом посмотрим), чтобы наша лыжа была какой-нибудь горбатой. Теперь давайте на неё посмотрим.

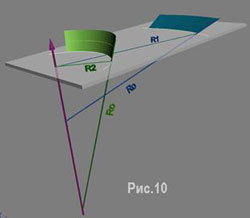
На рис. 9 нарисованы вместе две поверхности: та, что мы рассматривали в первой части, и коническая поверхность, опирающиеся на одну и ту же окружность поворота, так что их можно сравнить визуально. Эти поверхности соприкасаются по единственной линии, проходящей через точку «середины лыжи». Из рисунка также понятно, как должна изменяться коническая поверхность при изменении угла закантовки: если цилиндрическая поверхность наклоняется целиком, то у конической поверхности соответственно меняется угол раствора конуса.

Так вот, если бы лыжа была способна образовывать в процессе закантовки такую коническую поверхность, то у неё не было бы ни одной из ранее перечисленных «особенностей». Легко видеть, что коническая поверхность

образует один и то же угол с плоскостью основания, т.е. обеспечивает постоянный угол закантовки по всей длине лыжи,
если она заглублена в снег хоть по самую макушку, то не деформирует снег при повороте и испытывает только трение,
имеет одну и ту же кривую развертки для всех углов закантовки, и эта кривая (кривая бокового выреза) есть точно дуга окружности.

Последнее утверждение легко углядывается из простого геометрического построения, приведенного на рис. 10. Оно же показывает, как видоизменяется коническая поверхность в зависимости от угла закантовки. И известная зависимость радиуса поворота от радиуса бокового выреза и угла закантовки также вытекает из него элементарно.

Определенное скручивание для лыжи, как и пиво с утра, не только вредно, но и полезно

Каким же образом заставить лыжу изгибаться по конусу? Проще пареной репы свернуть из бумаги кулек, который тоже есть конус. Бумага может одинаково изгибаться по всем направлениям в плоскости листа, это и позволяет нам сворачивать её в конус. Но лыжа такими свойствами не обладает. Не можем же мы представить лыжу, которая скручивается в трубочку вокруг продольной оси. То есть, представить-то мы можем, но ездить на ней нельзя будет, как и на бумажной. Если поразмыслить над разверткой конуса, то становится ясно, что те палочки, которые мы старательно наклеивали на лыжу в начале первой части, должны быть расположены веером, а не параллельно друг другу, как у нас. А поскольку палочка ещё и обозначает направление, по которому может изгибаться лыжа, то единственный способ «сделать палки веером» - это изогнуть лыжу в боковом направлении. Ну, для этого, ясно, придётся идти к Head’у и падать в ножки: дескать, сделайте божескую милость, загните нам лыжу вот так-то и так-то. Поставят они пару-тройку микрочипов, лабуды всякой понавесят пьезоэлектрической, глядишь, и загнут родимую в бараний рог. Но пока не пойдем. Далеко. Давайте смотреть где-нибудь поближе.

Для начала вырежем из двух поверхностей на рис. 9 маленький кусочек, примерно соответствующий по длине лыже, и посмотрим на него как бы через волшебный прибор Левенгука. То, что мы примерно увидим, изображено на рис. 11.

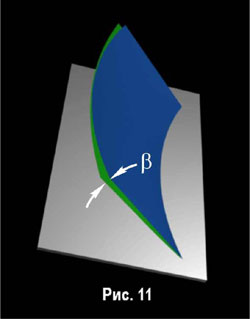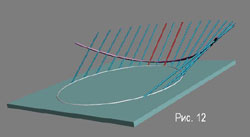
Из него видно, что обе наши поверхности соприкасаются по центру и по основанию, а их крайние кромки расходятся на некоторый угол, который мы для определенности будем называть β. Сразу же возникает здоровое подозрение, что если позволить концам нашей «идеальной» лыжи (синей) скручиваться при закантовке на угол β, то она, эта синяя поверхность, совпадет с зеленой, т.е. конической поверхностью. Чего, как бы, и хотелось. Это здоровое предположение и следует проверить.

[page]

Для этого мы должны перейти к следующему шагу и позволить лыже помимо прогиба дополнительно скручиваться вдоль продольной оси, т.е. дополнительно предположить некоторую торсионную податливость лыжи. Каким же образом будут теперь располагаться наши палочки в деформированном состоянии лыжи? Они уже не будут параллельными друг другу, но по-прежнему останутся прямыми и останутся перпендикулярными к продольной оси лыжи. Сама же ось уже не будет плоской кривой, а будет сложным образом изогнута в пространстве. И, прямо скажем, повторить наш эксперимент с хождением по кругу и втыканием в снег палочек будет в этом случае довольно затруднительным. Для этого придётся предварительно рассчитать, как и под какими углами какую палку втыкать. То есть делать такие противные вещи, которые ну никак не совмещаются с занимательностью нашей геометрии. Поэтому ограничимся частичной нарисованной картинкой, которая, может, и не совсем точна, но отражает характер деформации лыжи. Она приведена на рис. 12.

Что же мы можем из неё усмотреть? А то, что, вообще говоря, нам никогда не получить таким образом конической поверхности. То, что мы получили – не коническая поверхность. Попробуйте приложить карандаш к конической поверхности, например, ведра, так чтобы он касался её по всей длине. Это можно сделать только единственным образом: когда карандаш совпадает с образующей конуса. А у нас с образующей совпадает только одна палочка – та, которая находится между двумя красными. Так что в целом мы можем получить только некоторую изогнуто-скрученную поверхность, которая, если постараться, будет касательной к поверхности конуса по линии окружности поворота. Т.е. будет иметь тот же постоянный угол закантовки, что и у конуса. Что, в общем-то, тоже неплохо.

Угол β задает для данного угла закантовки величину оптимальной угловой деформации

Но. Наша лыжа не шибко большая. Она по длине тоже умещается между двух красных палочек. И в этой узкой области отклонение нашей поверхности от желаемой конусной настолько мало, что глазом не различишь. Так что можно считать, что мы своего добились, и лыжа с некоторой малой погрешностью принимает конусную форму.

На этом упражнения с лыжей можно считать законченными. Конечно, можно и дальше усложнять процесс деформации лыжи – заставить изгибаться ее в боковом направлении. Но жесткость лыжи на боковой изгиб весьма высока, и в реальности при закантовке практически не возникает сил, которые изгибали бы лыжу таким образом. А если и возникают, то действуют в противоположную от желаемой сторону.

Обратим ещё внимание на розовую линию на рис. 12. Она показывает, как изгибается продольная ось лыжи в случае деформации изгиба-скручивания. Это в целом довольно замысловато изогнутая пространственная линия, именуемая в геометрии «геодезической линией поверхности». Основное её свойство – наименьшее расстояние между двумя точками поверхности. И на развертке поверхности она превращается в прямую линию. Понятие это универсальное, и поэтому продольная ось лыжи всегда изгибается по геодезической той поверхности, которую лыжа образует при деформации. Поскольку наша поверхность все-таки близка к конусной, то получить практическое представление об общем характере такой линии можно, опоясав кожаным ремнем поверхность ведра так, чтобы он лежал без зазоров и нигде не морщил.

Что же следует из всего вышеизложенного? Из него следует то, что определенное скручивание для лыжи, как и пиво с утра, не только вредно, но и полезно. Если лыжа при закантовке будет одновременно с прогибом и скручиваться на угол, который мы определили как β, то от этого она станет только лучше. Это означает, что этот угол β, задает для данного угла закантовки величину оптимальной угловой деформации. Его можно рассчитать и использовать для определения нужных механических параметров лыжи. Этот угол меняется в зависимости от угла закантовки, как меняются и многие другие параметры, которые нужно учитывать: радиус поворота и действующие силы.

Этот угол меняется в зависимости от угла закантовки, как меняются и многие другие параметры, которые нужно учитывать: радиус поворота и действующие силы.

Взглянем снова на рис. 12. Из него видно, что все палочки проходят через точки окружности поворота благодаря согласованности деформаций изгиба и скручивания. Стоит изменить одну из них, как палочки уедут, и придётся подстраивать другую. Отвлечемся немного от геометрии и взглянем на это с точки зрения механики.

Чтобы лыжа скручивалась, допустим, в носке на некоторый угол, конструктору нужно обеспечить два параметра: определенный уровень торсионной жесткости, приведенной к носку лыжи, и определенный скручивающий момент. Скручивающий момент определяется шириной носка лыжи (а это геометрия) и действующей силой. Сила, в свою очередь, определяется изгибной жесткостью лыжи и величиной прогиба лыжи. Величина прогиба определяется величиной бокового выреза (и это тоже геометрия) и углом закантовки. Т.е. механические характеристики лыжи и параметры «плоской» геометрии круто перевязаны между собой. А «плоская» геометрия есть следствие геометрии «пространственной». И конструктору, которому приходится увязывать это всё между собой, не позавидуешь!

Что до нас, то наша геометрия чисто занимательная, и единственный полезный вывод из неё – это то, что к Head’у можно пока не ходить.

Обсудить статью можно здесь

Автор: Игорь Изыльметьев