 |
- «… именно геометрия, наверное, всегда
будет интересовать тех, кто увлечен
горными лыжами и относится к ним
немножко серьезнее, чем просто к способу
неплохо провести время …»
Георгий Дубенецкий «История геометрии»
Известно, что межсезонье для лыжника все равно, что менопауза. Прекращение активной выработки адреналина, наступающее вместе с исчезновением снега, нарушает сложившийся гормональный баланс организма, что ведет к негативным психофизиологическим последствиям. Хотя все естественные отправления и совершаются по-прежнему нормально, лыжник в это время становится вспыльчивым, быстро раздражается по пустякам и докучает домашним разным вздором про «большие горы и много снегу». Может даже начать копить деньги. Время от времени он испытывает приливы беспричинного гнева и начинает ругать Скиперфектума, факт божественного происхождения которого так и остался недоказанным, последними монгольскими словами. Бороться, конечно, можно. Одни пытаются подменить настоящий «снежный» адреналин суррогатом, вырабатываемым посредством различного рода экстрима на роликах и великах. Другие, чувствуя приближение симптомов, спасаются бегством в Южное полушарие, где как раз об это время северное. Слава богу, с первым снегом это всё проходит.
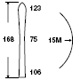
| Вся известная нам геометрия лыжи укладывается, в общем-то, в пять чисел, из которых только четыре являются независимыми |
Вся известная нам геометрия лыжи укладывается, в общем-то, в картинку, вынесенную в заголовок: пять чисел, из которых только четыре являются независимыми. Радиус бокового выреза определяется через четыре остальных размерности, или, если хочется, через радиус определяется что-нибудь другое. Эта, скажем, «плоская» геометрия варьируется от лыжи к лыже и в какой-то степени определяет их свойства.
Это, конечно же, далеко не вся геометрия лыжи, потому что все эти числа откуда-то берутся. И ещё что-то между ними чем-то заполняется - в смысле кривой бокового выреза. В качестве таковой, когда занималась карвинговая заря, были перепробованы всяческие экзотические кривые, вплоть до цепной линии. Но какой она должна быть и почему – вопрос опять же лыжной геометрии, которая куда более замысловата и занимательна, чем пять упомянутых чисел. И о которой нам почему-то никто не говорит. Возможно, не хотят нас огорчать. Поэтому придётся самим, по мере сил, в ней разбираться.
| Закантованная лыжа прогибается, кант лыжи ложится на поверхность склона и лыжа скользит по дуге прилегания канта к склону |
Итак, вслед за типовой геометрией обычно следует типовое описание механики резаного поворота на жестком склоне: закантованная лыжа прогибается, кант лыжи ложится на поверхность склона и лыжа скользит по дуге прилегания канта к склону, подобно лезвию конька (вообще говоря, сам я таких коньков не видел, они всё-таки как-то по-другому ездят, но сравнение красивое и в определённых случаях из него можно извлечь пользу).
Вот это описание и вызывает ряд «геометрических» вопросов:
- как прогибается лыжа?
- ложится ли кант на склон полностью или только частично?
- по какой дуге кант прилегает (если прилегает) к склону?
- и может ли лыжа по этой дуге скользить?
| Как прогибается лыжа? Ложится ли кант на склон полностью или только частично? |
Но для начала определимся с понятиями. Лыжа ставится на склон под углом (кантуется) и нагружается. С одной стороны – силами, действующими со стороны лыжника, с другой – силами, действующими со стороны снега. Под действием этих сил лыжа деформируется до тех пор, пока не ложится устойчиво на склон. Этот процесс мы далее будем именовать просто «закантовкой». Скользящая поверхность деформированной лыжи принимает при этом некоторую форму. Вот об этой форме далее и будет идти речь.
| По какой дуге кант прилегает (если прилегает) к склону? И может ли лыжа по этой дуге скользить? |
Так и будем поступать. Радиус мы, конечно, можем задать любой, но и 10 метров нас вполне устраивает. Скорость нас вообще не интересует в смысле геометрии, и угол закантовки мы можем задавать произвольно. (Но отметим подход специалиста: он берет один радиус поворота и один угол закантовки) А вот с «imagine» возникают серьёзные заморочки. Конечно, с лыжей одинаковой ширины нет проблем, а вот представить себе, как изгибается в повороте реальная лыжа, которая может гнуться и вдоль и поперек, и скручиваться при этом – это свыше способностей воображения автора. А что именно представляет себе Франко – он не уточнил. Поэтому придётся подбираться к этому самим, постепенно, мелкими шажками. Да и подготовить специнвентарь для опытов.
| Cut the ski with the snow surface, and there you are! |
Теперь мы можем и начинать. Но сначала придётся наложить на лыжу некоторые ограничения. Представим себе, что наша лыжа может только изгибаться как линейка, не скручиваясь и не прогибаясь в боковом плане. Это, к слову сказать, соответствует свойствам «идеальной лыжи», к которой вроде бы как стремятся все производители.
Что для неё характерно? То, что при всех возможных деформациях лыжи её продольная ось может изгибаться только в плоскости продольного сечения лыжи, т.е. только вверх и вниз и никак ни вправо, ни влево, А.все наши палочки остаются параллельными друг другу и перпендикулярными продольной оси лыжи.
Теперь нарисуем на снегу окружность поворота некоторого радиуса (да хоть те же 10 метров). Определимся с углом закантовки (например, 45 градусов). Поднесем нашу лыжу под этим углом к нарисованной окружности и начнем аккуратно втыкать её палочками в снег, начиная с середины и прогибая её так, чтобы каждая палочка втыкалась точно в нарисованную окружность. Как только все палочки будут воткнуты в снег, наступает момент «there you are!», для полного торжества которого достаточно пройтись ножовкой по палочкам точно по плоскости снега.
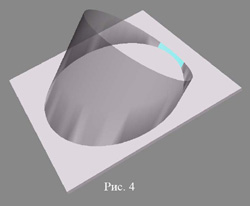
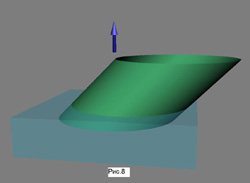
[page]Но не будем с этим спешить. Ещё успеем. Пока лыжа торчит в снегу, мы, имея солидный запас палочек, можем пройтись по нарисованной на снегу окружности поворота, втыкая через некоторые промежутки наши палочки так, чтобы и они оставались параллельными «лыжным» палочкам. В результате мы получим примерно такую картину, что изображена на рис.1.
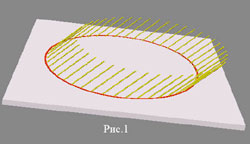 |
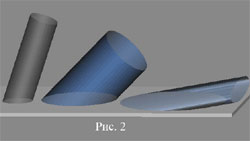
Все линии, из которых она образована, параллельны друг другу и наклонены к склону одинаково на один и тот же угол – угол закантовки. Поверхности, образованные параллельными линиями, называются цилиндрическими. Поскольку палочки обрезаны по одному уровню, то поверхность производит впечатление круглой. Но это не так.
 |
 |
 |
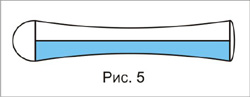 |
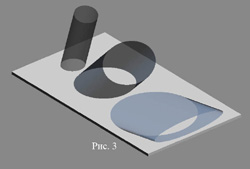
Попутно мы получили и ответ на вопрос, как прогибается такая лыжа. Она, т.е. её продольная ось, которая всегда перпендикулярна нашим палочкам, прогибается по дуге эллипса, лежащего в нормальном сечении поверхности, образуемой лыжей.
[page]Таким образом, лыжу мы нарисовали, и осталось что-нибудь сказать о её свойствах, которые прямо проистекают из общих свойств поверхности. Что до поверхности, то несколько настораживает то, что она не является поверхностью вращения, т.е. не обладает симметрией относительно оси поворота (случай угла закантовки в 90 градусов рассматривать не имеет смысла). От этого можно ожидать всяческих нюансов, которые мы сейчас постараемся усмотреть.
Ну, во-первых, на рис. 4, да и на остальных тоже, хорошо видно, что угол между плоскостью склона и внешней стороной нарисованной поверхности, который равен точно углу закантовки там, где у лыжи талия, дальше начинает увеличиваться и через четверть окружности поворота становится равным 90 град.;, а дальше увеличивается ещё больше. И это при любом произвольном угле закантовки. Само собой, и у лыжи то же самое, только в значительно меньшей степени, поскольку она составляет только малую часть окружности поворота. То есть угол закантовки лыжи изменяется по её длине, увеличиваясь от талии к концам лыжи. Что само по себе нехорошо, поскольку увеличение угла закантовки сверх необходимого приводит к увеличению давления на боковую сторону лыжи, что увеличивает сопротивление. Но мы не будем считать, сколько там градусов составляет это изменение, а просто отметим это обстоятельство.
 |
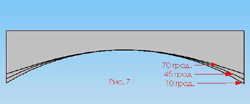 |
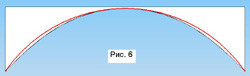
Как и следовало ожидать, они отличаются друг от друга. Отличия незначительны, но они есть. И чем «радикальней» лыжа, т.е. чем больше отношение её собственной длины к радиусу бокового выреза, тем сильнее проявляются эти эффекты. Что же это в целом означает? Это означает, что в рамках данной геометрии, которую может позволить себе наша «идеальная лыжа», мы можем точно построить кривую бокового выреза только для одного угла закантовки, или, если хотите, скорости. Для остальных углов она точной уже не будет.
 |
Вот такая геометрия у нас получается на данном этапе. Во второй части мы подумаем, что же со всем этим делать и куда грести.
Обсудить статью можно здесь
Автор: Игорь Изыльметьев
Другие статьи автора на сайте:
Лыжи и светлое будущее
Ещё раз про внутреннюю лыжу
Две оси на одно колено
Лыжные травмы коленей
Закантовка. Технический роман из жизни лыжи в двух частях с иллюстрациями
По следам «Пяти навыков…»
Виртуальный бугор и разгрузка вниз
Карвинговая лыжа. В поисках идеала





